How To Learn Trigonometry In One Day
Introduction to Trigonometry
Trigonometry (from Greek trigonon "triangle" + metron "measure")
Desire to learn Trigonometry? Here is a quick summary.
Follow the links for more, or get to Trigonometry Alphabetize
 | Trigonometry ... is all about triangles. |
Trigonometry helps united states find angles and distances, and is used a lot in science, engineering science, video games, and more!
Right-Angled Triangle
The triangle of about interest is the correct-angled triangle. The right bending is shown by the little box in the corner:

Another angle is ofttimes labeled θ, and the 3 sides are then called:
- Side by side: side by side (side by side to) the bending θ
- Opposite: reverse the angle θ
- and the longest side is the Hypotenuse
Why a Right-Angled Triangle?
Why is this triangle so important?
Imagine we tin measure along and upward but desire to know the straight altitude and angle:

Trigonometry can find that missing angle and distance.
Or perhaps we have a altitude and angle and need to "plot the dot" along and up:

Questions like these are mutual in applied science, calculator animation and more than.
And trigonometry gives the answers!
Sine, Cosine and Tangent
The main functions in trigonometry are Sine, Cosine and Tangent
They are simply one side of a right-angled triangle divided by another.
For whatever angle " θ ":

(Sine, Cosine and Tangent are oftentimes abbreviated to sin, cos and tan.)
Case: What is the sine of 35°?
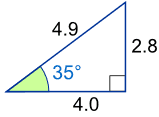
Using this triangle (lengths are merely to one decimal place):
sin(35°) = Contrary Hypotenuse = two.8 iv.9 = 0.57...
The triangle could be larger, smaller or turned around, but that angle will ever take that ratio.
Calculators have sin, cos and tan to assistance united states, and then let'south see how to utilise them:

Case: How Tall is The Tree?
Nosotros can't reach the top of the tree, and so we walk away and mensurate an angle (using a protractor) and distance (using a laser):
- We know the Hypotenuse
- And we want to know the Opposite
Sine is the ratio of Opposite / Hypotenuse:
sin(45°) = Reverse Hypotenuse

Go a calculator, blazon in "45", then the "sin" key:
sin(45°) = 0.7071...
What does the 0.7071... mean? It is the ratio of the side lengths, and so the Opposite is virtually 0.7071 times every bit long every bit the Hypotenuse.
We tin can now put 0.7071... in place of sin(45°):
0.7071... = Opposite Hypotenuse
And nosotros also know the hypotenuse is 20:
0.7071... = Opposite xx
To solve, first multiply both sides past 20:
20 × 0.7071... = Opposite
Finally:
Opposite = xiv.14m (to two decimals)

Case: How Tall is The Tree?
Start with: sin(45°) = Opposite Hypotenuse
We know: 0.7071... = Opposite xx
Swap sides: Opposite 20 = 0.7071...
Multiply both sides by 20: Opposite = 0.7071... × twenty
Calculate: Opposite = 14.14
(to 2 decimals)
The tree is 14.14m tall
Try Sin Cos and Tan
Play with this for a while (motion the mouse around) and become familiar with values of sine, cosine and tangent for dissimilar angles, such as 0°, 30°, 45°, threescore° and 90°.
../algebra/images/circle-triangle.js
Also effort 120°, 135°, 180°, 240°, 270° etc, and find that positions can exist positive or negative by the rules of Cartesian coordinates, so the sine, cosine and tangent change between positive and negative also.
So trigonometry is besides about circles!

Unit Circumvolve
What y'all just played with is the Unit Circle.
It is a circle with a radius of 1 with its heart at 0.
Because the radius is 1, we tin can straight measure sine, cosine and tangent.
Here nosotros come across the sine function beingness made by the unit circle:
images/circle-sine.js
Notation: y'all can encounter the nice graphs made by sine, cosine and tangent.
Degrees and Radians
Angles can exist in Degrees or Radians. Here are some examples:
Repeating Design
Because the angle is rotating around and around the circle the Sine, Cosine and Tangent functions repeat once every full rotation (see Amplitude, Menstruation, Phase Shift and Frequency).

When we want to calculate the part for an angle larger than a full rotation of 360° (twoπ radians) nosotros decrease equally many full rotations equally needed to bring it back below 360° (2π radians):
Example: what is the cosine of 370°?
370° is greater than 360° so let us subtract 360°
370° − 360° = 10°
cos(370°) = cos(10°) = 0.985 (to iii decimal places)
And when the angle is less than cypher, only add total rotations.
Example: what is the sine of −3 radians?
−three is less than 0 then allow us add twoπ radians
−three + 2π = −iii + 6.283... = 3.283... radians
sin(−3) = sin(3.283...) = −0.141 (to 3 decimal places)
Solving Triangles
Trigonometry is too useful for general triangles, not just right-angled ones .
It helps us in Solving Triangles. "Solving" ways finding missing sides and angles.
We can also detect missing side lengths. The general dominion is:
When nosotros know whatever iii of the sides or angles we can find the other 3
(except for the three angles case)
Come across Solving Triangles for more details.
Other Functions (Cotangent, Secant, Cosecant)
Similar to Sine, Cosine and Tangent, there are three other trigonometric functions which are fabricated past dividing ane side by some other:

| Cosecant Office: | csc(θ) = Hypotenuse / Contrary |
| Secant Function: | sec(θ) = Hypotenuse / Adjacent |
| Cotangent Function: | cot(θ) = Adjacent / Reverse |
Trigonometric and Triangle Identities
And as yous get better at Trigonometry you lot can acquire these:
Enjoy becoming a triangle (and circumvolve) proficient!
How To Learn Trigonometry In One Day,
Source: https://www.mathsisfun.com/algebra/trigonometry.html
Posted by: grahamthein2000.blogspot.com


0 Response to "How To Learn Trigonometry In One Day"
Post a Comment